An Empirical Exploration of Gradient Correlations in Deep Learning
Daniel Rothchild, Roy Fox, Noah Golmant, Joseph Gonzalez, Michael Mahoney, Kai Rothauge, Ion Stoica, and Zhewei Yao
Integration of Deep Learning Theories workshop (DLT @ NeurIPS), 2018
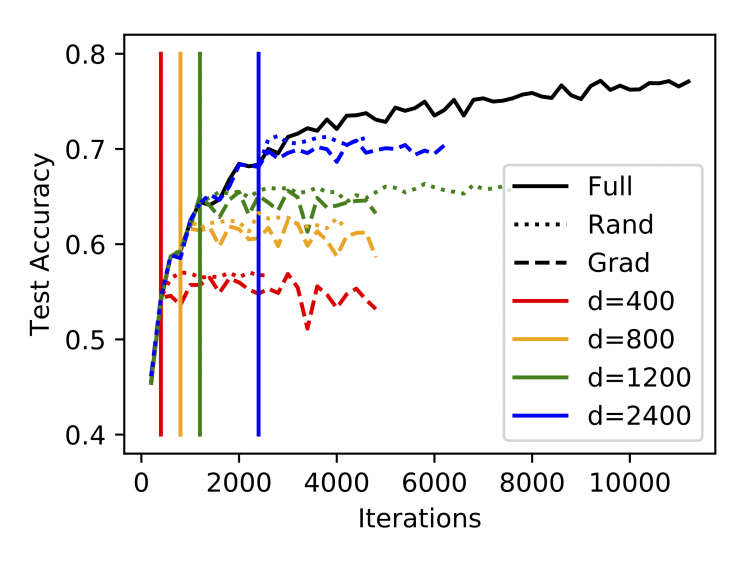
We introduce the mean and RMS dot product between normalized gradient vectors as tools for investigating the structure of loss functions and the trajectories followed by optimizers. We show that these quantities are sensitive to well-understood properties of the optimization algorithm, and we argue that investigating these quantities in detail can provide insight into properties that are less well understood. Using these tools, we observe that variance in the gradients of the loss function can be mostly explained by a small number of dimensions, and we compare results when training networks within the subspace spanned by the first few gradients to those obtained by training within a randomly chosen subspace.